Lecture 4 - Learning control laws with Dynamical Systems
Abstract
This lecture details methods to learn a control law for robot motion generation using time-invariant dynamical systems (DSs). Our training data consists of sample trajectories, which cover a limited portion of the state space. The goal of the learning algorithm is to reproduce the training data well, while generalizing over the rest of the workspace. In particular, we must ensure that the system does not diverge from the training data. In short, we wish to learn a function which reproduces the provided reference dynamics and converges to a single stable equilibrium point, also called the target or attractor.
Lecture Videos
Slides
Click the links below to download a pdf version of the ppt presentations.
Exercises Instructions
Click here to download a pdf of the instructions for the exercises.
Code for MATLAB Exercises
The recommended way to do the MATLAB exercises is to download the entire repository once, then go to each lecture's folder. Detailled instructions for installation can be found on the Software page.
Click here to download the corresponding exercise for this lecture as a zip file.
Note you will also need this libraries folder placed with the correct directory structure.
First Theoretical Exercise Solution
Click here to download a pdf of the solution of the first handwritten exercise.
Supplements
SEDS implementation
LPV-DS implementation
Multi-attractor DS
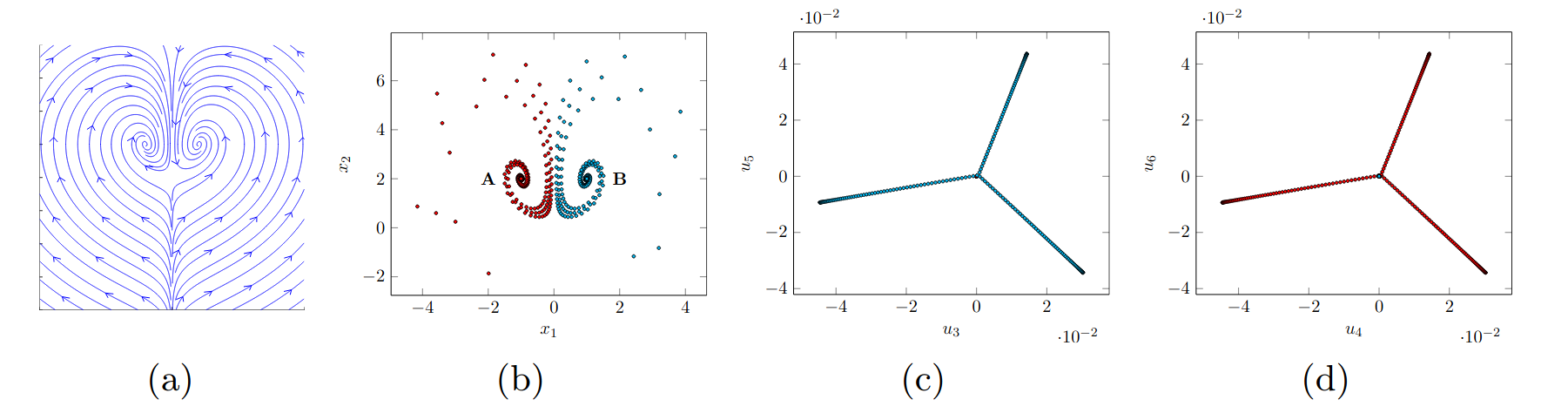
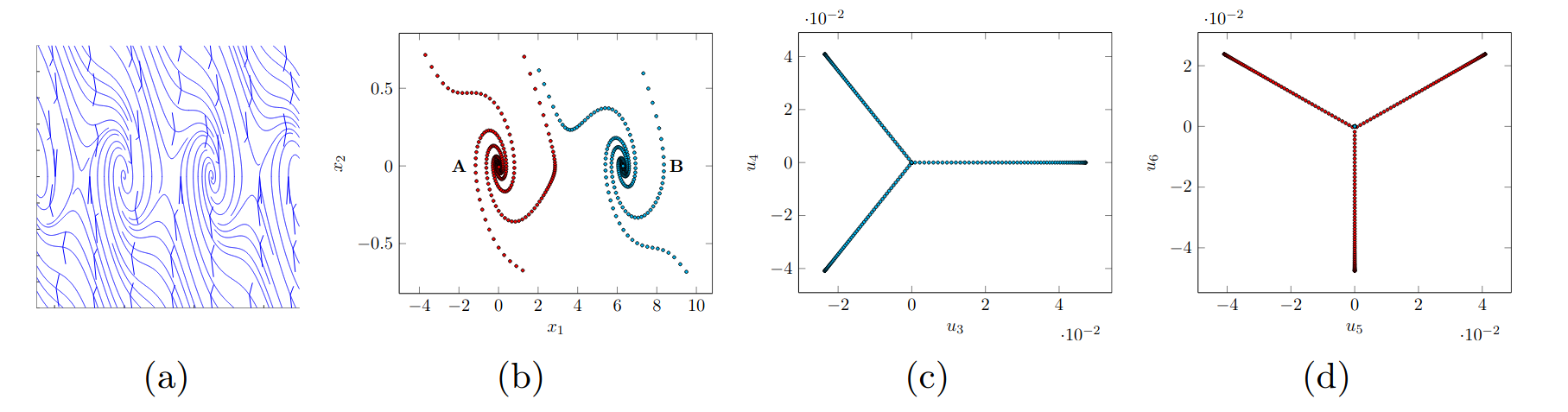
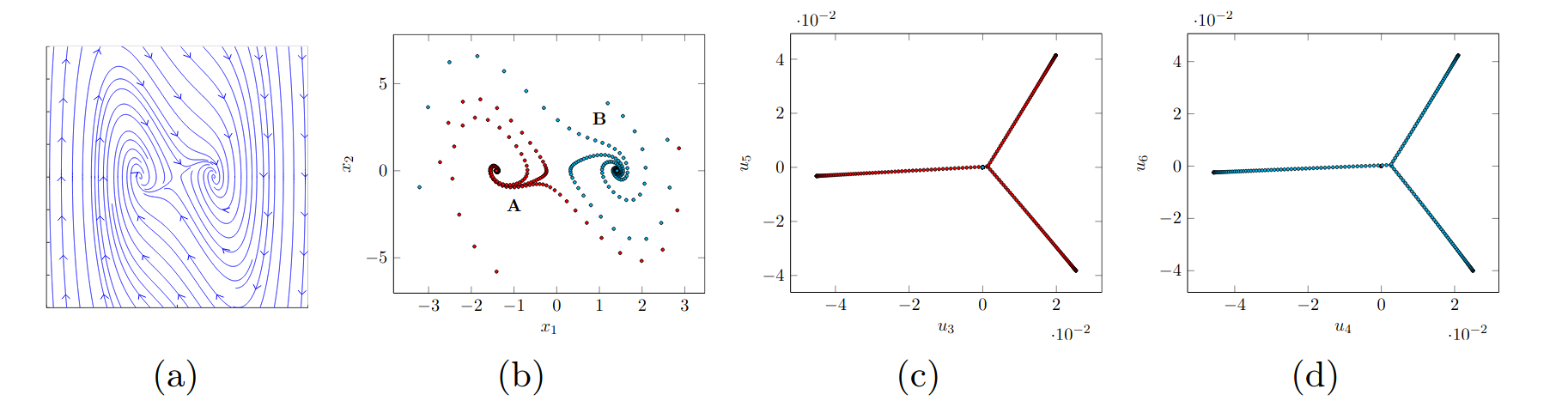
(a) Original Vector field (b) Sub-Sampled trajectories from the DS. (c) Embedding space of the sub-dynamics with a local attractor. (d) Embedding space of the sub-dynamics with a local attractor.
We propose a Graph-based spectral clustering method that takes advantage of a velocity-augmented kernel to connect data points belonging to the same dynamics, while preserving the natural temporal evolution. We study the eigenvectors and eigenvalues of the Graph Laplacian and show that they form a set of orthogonal embedding spaces, one for each sub-dynamics. We prove that there always exist a set of 2-dimensional embedding spaces in which the sub-dynamics are linear and n-dimensional embedding spaces where they are quasi-linear. We learn a diffeomorphism from the Laplacian embedding space to the original space and show that the Laplacian embedding leads to good reconstruction accuracy and a faster training time through an exponential decaying loss compared to the state-of-the-art diffeomorphism-based approaches.
Dynamical system approach to navigation around obstacles
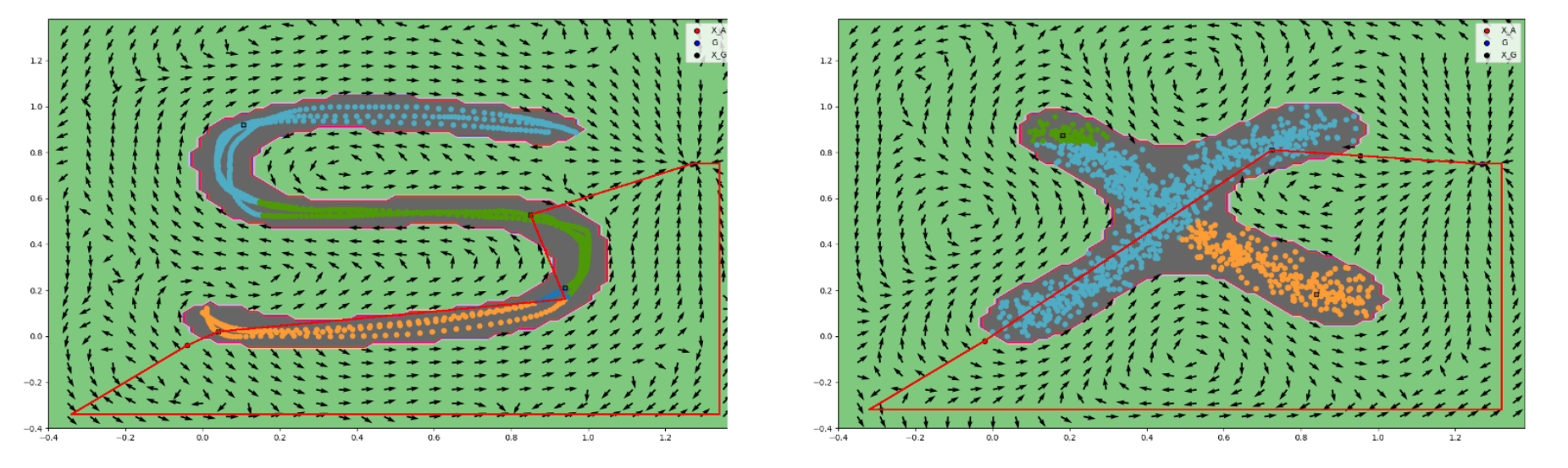
In this article, we propose a dynamical system to avoid obstacles which are star shaped and simultaneously converge to a goal. The convergence is almost-global in a domain and the stationary points are identified explicitly. Our approach is based on the idea that an ideal vector field which avoids the obstacle traverses its boundary up to when a clear path to the goal is available. We show the existence of this clear path through a set connecting the boundary of the obstacle and the goal. We verify the theoretical results presented with various hand drawn obstacle sets. Our methodology is also extended to obstacles which are not star-shaped, and, those which exist in high dimensions.
